在《张朝阳的物理课》的直播中,张朝阳深入浅出地讲解了量子力学中的核心问题——氢原子的薛定谔方程。本文将聚焦于该课程中关于薛定谔方程角向部分的求解,探讨其理论背景、数学方法及其物理意义。
1. 薛定谔方程与氢原子
薛定谔方程是量子力学的基石,描述了微观粒子如电子的运动状态。对于氢原子,薛定谔方程可以精确求解,这是量子力学早期成功应用的典范。氢原子的薛定谔方程可以分为径向部分和角向部分,其中角向部分主要描述电子在原子核周围的角动量分布。
2. 角向部分的数学形式
角向部分的薛定谔方程通常表示为拉普拉斯算子的角向部分,即:
\[ \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} \left( \sin \theta \frac{\partial}{\partial \theta} \right) \frac{1}{\sin^2 \theta} \frac{\partial^2}{\partial \phi^2} \]
其中,\(\theta\) 和 \(\phi\) 是球坐标系中的角度变量。求解这一部分方程,需要利用球谐函数 \(Y_{l}^{m}(\theta, \phi)\),它们是角向方程的解,并且满足正交归一性。
3. 球谐函数的性质与求解
球谐函数 \(Y_{l}^{m}(\theta, \phi)\) 是角动量算符的本征函数,其中 \(l\) 是角动量量子数,\(m\) 是磁量子数。它们的形式可以通过求解上述角向拉普拉斯算子得到,具体形式为:
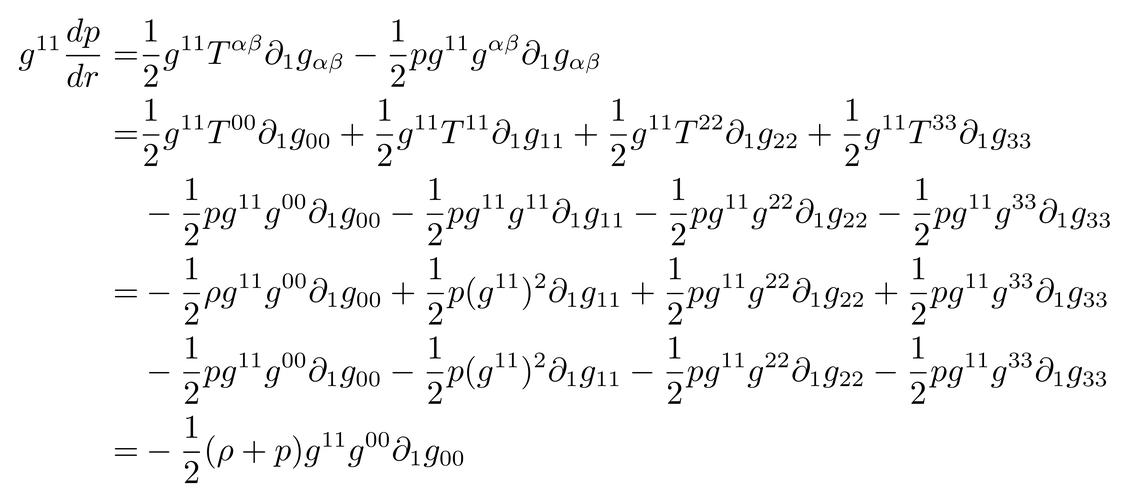
\[ Y_{l}^{m}(\theta, \phi) = (1)^{(m |m|)/2} \sqrt{\frac{2l 1}{4\pi} \frac{(l|m|)!}{(l |m|)!}} P_l^{|m|}(\cos \theta) e^{im\phi} \]
其中,\(P_l^{|m|}(\cos \theta)\) 是伴随勒让德多项式。球谐函数不仅在数学上具有优美的对称性,而且在物理上描述了电子云在空间中的分布,是理解原子光谱和化学键的关键。
4. 物理意义与应用
通过求解薛定谔方程的角向部分,我们可以得到氢原子中电子的角向分布,这对于理解原子的化学性质和光谱特性至关重要。例如,不同的 \(l\) 值对应不同的电子轨道形状,如 \(s\) 轨道(\(l=0\))为球形,\(p\) 轨道(\(l=1\))为哑铃形等。这些轨道的空间分布直接影响了原子间的相互作用和化学反应。
5. 结论
在《张朝阳的物理课》中,对氢原子薛定谔方程角向部分的深入讨论,不仅展示了量子力学的数学之美,也揭示了其深刻的物理内涵。通过精确求解角向方程,我们能够更深入地理解原子结构和量子世界的奇妙规律。这一过程不仅是对理论物理的一次探索,也是对自然界基本规律的一次深刻洞察。
通过这篇文章,我们希望读者能够对氢原子薛定谔方程的角向部分有一个清晰的理解,并感受到量子力学在解释微观世界中的强大力量。