在物理学中,磁场的性质一直是研究的重点之一。特别是磁感应强度(B)的散度等于零这一特性,不仅是磁场理论的核心,也是麦克斯韦方程组的重要组成部分。本文将通过介绍毕奥萨伐尔定律,探讨磁感应强度散度为何等于零,并解释这一特性在物理学中的重要意义。
1. 毕奥萨伐尔定律简介
毕奥萨伐尔定律是电磁学中的基本定律之一,它描述了电流元在空间中产生磁场的规律。根据毕奥萨伐尔定律,一个电流元 \( I \mathrm{d}\boldsymbol{l} \) 在空间某点产生的磁场 \(\mathrm{d}\boldsymbol{B}\) 可以表示为:
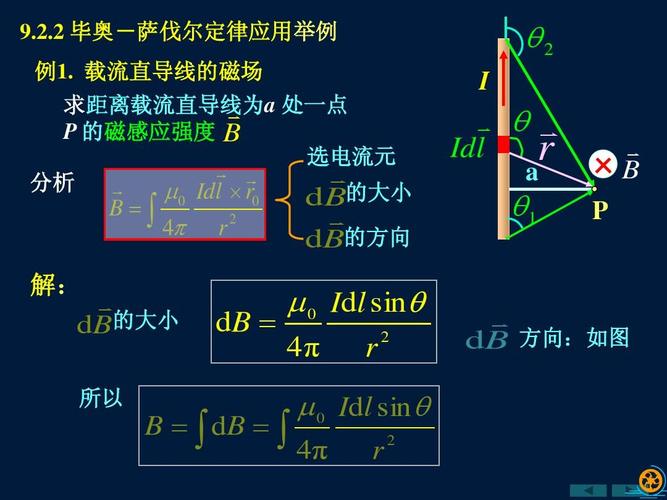
\[ \mathrm{d}\boldsymbol{B} = \frac{\mu_0}{4\pi} \frac{I \mathrm{d}\boldsymbol{l} \times \boldsymbol{r}}{r^3} \]
其中,\( \mu_0 \) 是真空磁导率,\( \boldsymbol{r} \) 是从电流元到场点的位置矢量,\( r \) 是 \( \boldsymbol{r} \) 的模长。
2. 磁感应强度的散度
磁感应强度 \(\boldsymbol{B}\) 的散度定义为:
\[ \nabla \cdot \boldsymbol{B} = \lim_{\Delta V \to 0} \frac{\oint_S \boldsymbol{B} \cdot \mathrm{d}\boldsymbol{S}}{\Delta V} \]
其中,\( \Delta V \) 是体积元,\( S \) 是 \( \Delta V \) 的表面。
为了计算 \(\nabla \cdot \boldsymbol{B}\),我们可以考虑一个由电流元产生的磁场,并对其进行积分。根据毕奥萨伐尔定律,磁场 \(\boldsymbol{B}\) 是旋转对称的,且与位置矢量 \( \boldsymbol{r} \) 垂直。因此,当对 \(\boldsymbol{B}\) 进行散度运算时,由于 \(\boldsymbol{B}\) 的矢量性质,其散度将主要取决于 \( \boldsymbol{B} \) 在不同方向上的变化。
3. 磁感应强度散度为零的证明
考虑一个闭合曲面 \( S \),其内部包含多个电流元。根据毕奥萨伐尔定律,每个电流元产生的磁场都是旋转对称的,且在闭合曲面上的积分将相互抵消。这是因为,对于任意一个电流元,其在闭合曲面上的磁场线总是成对出现,且方向相反。因此,整个闭合曲面上的磁场积分等于零。
由于闭合曲面 \( S \) 是任意选取的,这意味着在空间中任意点的磁感应强度散度都等于零,即:
\[ \nabla \cdot \boldsymbol{B} = 0 \]
4. 物理意义与应用
磁感应强度散度为零这一特性,表明磁场是无源场。这与电场形成鲜明对比,电场是有源场,其散度不为零。这一特性在电磁学中有着广泛的应用,尤其是在麦克斯韦方程组的构建中。麦克斯韦方程组中的安培定律修正项就是基于磁感应强度散度为零这一事实。
磁感应强度散度为零还意味着磁场线总是闭合的,不存在磁单极子。这一结论在现代物理学中仍然是一个重要的未解之谜,因为理论物理学家在某些理论模型中预言了磁单极子的存在。
5. 结论
通过毕奥萨伐尔定律,我们不仅理解了电流元如何产生磁场,还揭示了磁感应强度散度为零这一重要物理特性。这一特性不仅是磁场理论的基础,也是理解电磁现象的关键。随着物理学的发展,对磁场性质的深入研究将继续推动我们对自然界的认识。